Model fitting toolbox¶
The model fitting toolbox uses the package Playdoh, you can see the documentation here.
-
brian.library.modelfitting.modelfitting(**kwds)¶ Model fitting function.
Fits a spiking neuron model to electrophysiological data (injected current and spikes).
See also the section Model fitting in the user manual.
Arguments
model- An
Equationsobject containing the equations defining the model. reset- A reset value for the membrane potential, or a string containing the reset equations.
threshold- A threshold value for the membrane potential, or a string containing the threshold equations.
refractoryThe refractory period in second. If it’s a single value, the same refractory will be used in all the simulations. If it’s a list or a tuple, the fitting will also optimize the refractory period (see
**paramsbelow).Warning: when using a refractory period, you can’t use a custom reset, only a fixed one.
data- A list of spike times, or a list of several spike trains as a list of pairs (index, spike time) if the fit must be performed in parallel over several target spike trains. In this case, the modelfitting function returns as many parameters sets as target spike trains.
input_var='I'- The variable name used in the equations for the input current.
input- A vector of values containing the time-varying signal the neuron responds to (generally an injected current).
dt- The time step of the input (the inverse of the sampling frequency).
**paramsThe list of parameters to fit the model with. Each parameter must be set as follows:
param_name=[bound_min, min, max, bound_max]wherebound_minandbound_maxare the boundaries, andminandmaxspecify the interval from which the parameter values are uniformly sampled at the beginning of the optimization algorithm. If not using boundaries, setparam_name=[min, max].Also, you can add a fit parameter which is a spike delay for all spikes : add the special parameter
delaysin**params, for examplemodelfitting(..., delays=[-10*ms, 10*ms]).You can also add fit the refractory period by specifying
modelfitting(..., refractory=[-10*ms, 10*ms]).popsize- Size of the population (number of particles) per target train used by the optimization algorithm.
maxiter- Number of iterations in the optimization algorithm.
optparams- Optimization algorithm parameters. It is a dictionary: keys are parameter names,
values are parameter values or lists of parameters (one value per group).
This argument is specific to the optimization
algorithm used. See
PSO,GA,CMAES. delta=4*ms- The precision factor delta (a scalar value in second).
slices=1- The number of time slices to use.
overlap=0*ms- When using several time slices, the overlap between consecutive slices, in seconds.
initial_values- A dictionary containing the initial values for the state variables.
cpu- The number of CPUs to use in parallel. It is set to the number of CPUs in the machine by default.
gpu- The number of GPUs to use in parallel. It is set to the number of GPUs in the machine by default.
precision- GPU only: a string set to either
floatordoubleto specify whether to use single or double precision on the GPU. If it is not specified, it will use the best precision available. returninfo=False- Boolean indicating whether the modelfitting function should return technical information about the optimization.
scaling=None- Specify the scaling used for the parameters during the optimization.
It can be
Noneor'mapminmax'. It isNoneby default (no scaling), andmapminmaxby default for the CMAES algorithm. algorithm=CMAES- The optimization algorithm. It can be
PSO,GAorCMAES. optparams={}- Optimization parameters. See
method='Euler'- Integration scheme used on the CPU and GPU:
'Euler'(default),RK, orexponential_Euler. See also Numerical integration. machines=[]- A list of machine names to use in parallel. See Clusters.
Return values
Return an
OptimizationResultobject with the following attributes:best_pos- Minimizing position found by the algorithm. For array-like fitness functions, it is a single vector if there is one group, or a list of vectors. For keyword-like fitness functions, it is a dictionary where keys are parameter names and values are numeric values. If there are several groups, it is a list of dictionaries.
best_fit- The value of the fitness function for the best positions. It is a single value if there is one group, or it is a list if there are several groups.
info- A dictionary containing various information about the optimization.
Also, the following syntax is possible with an
OptimizationResultinstanceor. Thekeyis either an optimizing parameter name for keyword-like fitness functions, or a dimension index for array-like fitness functions.or[key]- it is the best
keyparameter found (single value), or the list of the best parameterskeyfound for all groups. or[i]- where
iis a group index. This object has attributesbest_pos,best_fit,infobut only for groupi. or[i][key]- where
iis a group index, is the same asor[i].best_pos[key].
For more details on the gamma factor, see Jolivet et al. 2008, “A benchmark test for a quantitative assessment of simple neuron models”, J. Neurosci. Methods (available in PDF here).
-
brian.library.modelfitting.print_table(results, precision=4, colwidth=16)¶ Displays the results of an optimization in a table.
Arguments:
results- The results returned by the
minimizeofmaximizefunction. precision = 4- The number of decimals to print for the parameter values.
colwidth = 16- The width of the columns in the table.
-
brian.library.modelfitting.open_server(port=None, maxcpu=None, maxgpu=None, local=None)¶ Start the Playdoh server.
Arguments:
port=DEFAULT_PORT- The port (integer) of the Playdoh server. The default is DEFAULT_PORT, which is 2718.
maxcpu=MAXCPU- The total number of CPUs the Playdoh server can use.
MAXCPUis the total number of CPUs on the computer. maxgpu=MAXGPU- The total number of GPUs the Playdoh server can use.
MAXGPUis the total number of GPUs on the computer, if PyCUDA is installed.
-
brian.library.modelfitting.get_spikes(model=None, reset=None, threshold=None, input=None, input_var='I', dt=None, initial_values=None, **params)¶ Retrieves the spike times corresponding to the best parameters found by the modelfitting function.
Arguments
model,reset,threshold,input,input_var,dt,initial_values- Same parameters as for the
modelfittingfunction. **params- The best parameters returned by the
modelfittingfunction.
Returns
spiketimes- The spike times of the model with the given input and parameters.
-
brian.library.modelfitting.predict(model=None, reset=None, threshold=None, data=None, delta=4.0 * msecond, input=None, input_var='I', dt=None, **params)¶ Predicts the gamma factor of a fitted model with respect to the data with a different input current.
Arguments
model,reset,threshold,input_var,dt- Same parameters as for the
modelfittingfunction. input- The input current, that can be different from the current used for the fitting procedure.
data- The experimental spike times to compute the gamma factor against. They have
been obtained with the current
input. **params- The best parameters returned by the
modelfittingfunction.
Returns
gamma- The gamma factor of the model spike trains against the data. If there were several groups in the fitting procedure, it is a vector containing the gamma factor for each group.
-
class
brian.library.modelfitting.PSO¶ Particle Swarm Optimization algorithm. See the wikipedia entry on PSO.
Optimization parameters:
omega- The parameter
omegais the “inertial constant” clclis the “local best” constant affecting how much the particle’s personal best position influences its movement.cgcgis the “global best” constant affecting how much the global best position influences each particle’s movement.
See the wikipedia entry on PSO for more details (note that they use
c_1andc_2instead ofclandcg). Reasonable values are (.9, .5, 1.5), but experimentation with other values is a good idea.
-
class
brian.library.modelfitting.GA¶ Standard genetic algorithm. See the wikipedia entry on GA
If more than one worker is used, it works in an island topology, i.e. as a coarse-grained parallel genetic algorithms which assumes a population on each of the computer nodes and migration of individuals among the nodes.
Optimization parameters:
proportion_parents=1- proportion (out of 1) of the entire population taken as potential parents.
migration_time_interval=20- whenever more than one worker is used, it is the number of iteration at which a migration happens . (note for different groups case: this parameter can only have one value, i.e. every group will have the same value (the first of the list))
proportion_migration=0.2- proportion (out of 1) of the island population that will migrate to the next island (the best one) and also the worst that will be replaced by the best of the previous island. (note for different groups case: this parameter can only have one value, i.e. every group will have the same value (the first of the list))
proportion_xover=0.65- proportion (out of 1) of the entire population which will undergo a cross over.
proportion_elite=0.05proportion (out of 1) of the entire population which will be kept for the next generation based on their best fitness.
The proportion of mutation is automatically set to
1-proportion_xover-proportion_elite.func_selection='stoch_uniform'- This function define the way the parents are chosen (it is the only one available). It lays out a line in which each parent corresponds to a section of the line of length proportional to its scaled value. The algorithm moves along the line in steps of equal size. At each step, the algorithm allocates a parent from the section it lands on. The first step is a uniform random number less than the step size.
func_xover='intermediate'func_xoverspecifies the function that performs the crossover. The following ones are available:intermediate: creates children by taking a random weighted average of the parents. You can specify the weights by a single parameter,``ratio_xover`` (which is 0.5 by default). The function creates the child from parent1 and parent2 using the following formula:
child = parent1 + rand * Ratio * ( parent2 - parent1)
discrete_random: creates a random binary vector and selects the genes where the vector is a 1 from the first parent, and the genes where the vector is a 0 from the second parent, and combines the genes to form the child.
one_point: chooses a random integer n between 1 and ndimensions and then selects vector entries numbered less than or equal to n from the first parent. It then Selects vector entries numbered greater than n from the second parent. Finally,it concatenates these entries to form a child vector.
two_points: it selects two random integers m and n between 1 and ndimensions. The function selects vector entries numbered less than or equal to m from the first parent. Then it selects vector entries numbered from m+1 to n, inclusive, from the second parent. Then it selects vector entries numbered greater than n from the first parent. The algorithm then concatenates these genes to form a single gene.
heuristic: returns a child that lies on the line containing the two parents, a small distance away from the parent with the better fitness value in the direction away from the parent with the worse fitness value. You can specify how far the child is from the better parent by the parameter
ratio_xover(which is 0.5 by default)linear_combination: creates children that are linear combinations of the two parents with the parameter
ratio_xover(which is 0.5 by default and should be between 0 and 1):child = parent1 + Ratio * ( parent2 - parent1)
For
ratio_xover=0.5every child is an arithmetic mean of two parents.
func_mutation='gaussian'This function define how the genetic algorithm makes small random changes in the individuals in the population to create mutation children. Mutation provides genetic diversity and enable the genetic algorithm to search a broader space. Different options are available:
gaussian: adds a random number taken from a Gaussian distribution with mean 0 to each entry of the parent vector.
The ‘scale_mutation’ parameter (0.8 by default) determines the standard deviation at the first generation by
scale_mutation*(Xmax-Xmin)where Xmax and Xmin are the boundaries.The ‘shrink_mutation’ parameter (0.2 by default) controls how the standard deviation shrinks as generations go by:
:math:`\sigma_{i}=\sigma_{i-1}(1-shrink_{mutation}*i/maxiter)` at iteration i.uniform: The algorithm selects a fraction of the vector entries of an individual for mutation, where each entry has a probability
mutation_rate(default is 0.1) of being mutated. In the second step, the algorithm replaces each selected entry by a random number selected uniformly from the range for that entry.
-
class
brian.library.modelfitting.CMAES¶ Covariance Matrix Adaptation Evolution Strategy algorithm See the wikipedia entry on CMAES and also the author’s website <http://www.lri.fr/~hansen/cmaesintro.html>`
Optimization parameters:
proportion_selective=0.5- This parameter (refered to as mu in the CMAES algorithm) is the proportion (out of 1) of the entire population that is selected and used to update the generative distribution. (note for different groups case: this parameter can only have one value, i.e. every group will have the same value (the first of the list))
bound_strategy=1:In the case of a bounded problem, there are two ways to handle the new generated points which fall outside the boundaries. (note for different groups case: this parameter can only have one value, i.e. every group will have the same value (the first of the list))
bound_strategy=1. With this strategy, every point outside the domain is repaired, i.e. it is projected to its nearset possible value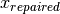 .
In other words, components that are infeasible in
.
In other words, components that are infeasible in 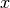 are set to the (closest) boundary value in
are set to the (closest) boundary value in 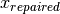 .
The fitness function on the repaired search points is evaluated and a penalty which depends on the distance to the repaired solution is added
.
The fitness function on the repaired search points is evaluated and a penalty which depends on the distance to the repaired solution is added
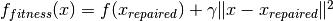
The repaired solution is disregarded afterwards.
bound_strategy=2With this strategy any infeasible solution x is resampled until it become feasible. It should be used only if the optimal solution is not close to the infeasible domain.See p.28 of <http://www.lri.fr/~hansen/cmatutorial.pdf> for more details
gammagammais the weight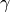 in the previously introduced penalty function. (note for different groups case: this parameter can only have one value, i.e. every group
will have the same value (the first of the list))
in the previously introduced penalty function. (note for different groups case: this parameter can only have one value, i.e. every group
will have the same value (the first of the list))